Ciąg Fibonacciego

   Leonardo Fibonacci, włoski matematyk pochodzący z Pizy, żył w latach 1175-1250. Kształcił się początkowo po kierunkiem arabskiego nauczyciela na terenie obecnej algierskiej Beżai. W miarę postępów nauki i chęci dalszego studiowania zwiedził Europę i kraje Wschodu. Podczas swych podróży zapoznał się z osiągnięciami arabskich i hinduskich matematyków, między innymi z systemem dziesiętnym, który później propagował.

   Gdy w 1202 roku wrócił do kraju, do Pizy, opisał system pozycyjny liczb i wyłożył podstawy arytmetyki w dziele zatytułowanym „Liber Abaci”, czyli „Księga rachunków”. Tu właśnie Fibonacci  pisał, i to od pierwszych stron, o cyfrach arabskich. W swojej kolejnej pracy – „Practica geometriae” uczony połączył geometrię i algebrę.
   W późniejszych latach Fibonacci zajmował się między innymi arytmetyką handlową, opracowywał metody rozwiązywania zadań z tej dziedziny oparte na proporcjach. Nauczał działań na ułamkach, które sprowadzał do wspólnego mianownika w sposób bardziej racjonalny, niż robili to matematycy krajów islamu – otóż znajdował najmniejszą wspólną wielokrotność mianowników.

   Fibonacci niezwykle pilnie studiował matematykę, umiał ją także wzbogacać. Wprawdzie jego prace, które dotyczyły teorii liczb, musiały czekać na kontynuację ponad czterysta lat, ale jego nazwisko weszło do matematyki – głównie dzięki ciągowi liczb, nazwanemu od jego nazwiska ciągiem Fibonacciego – za sprawą XIX-wiecznego francuskiego matematyka Edwarda Lucasa.
Ciąg Fibonacciego to ciąg liczb naturalnych określonych w taki oto sposób:
   F0 = 0,  F1 = 1,  Fn = Fn-1 + Fn-2, dla n ≥ 2
   Pierwsze jego wartości to:
   0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, ...
   Jakie są własności tego ciągu? Między innymi jest to ciąg resurcyjny, inaczej mówiąc – rekurencyjny, definiujący sam siebie. Każda z liczb w ciągu Fibonacciego (poza wartościami stałymi 0 i 1) jest sumą dwóch poprzednich, np.:
   3 + 5 = 8,  21 + 34 = 55,  144 + 233 = 377...
   Do interesujących właściwości ciągu należy również ta, że jeżeli podzielimy dowolną liczbę ciągu przez jej poprzednik, za każdym razem otrzymany wynik waha się w okolicach 1,618 – w miarę zwiększania się liczb iloraz zbliża się do tej wartości, np.:
   21 : 13 = 1,615,  987 : 610 = 1,618...
Natomiast wynik podzielenia każdej z liczb przez następną w ciągu waha się wokół odwrotności 1,618, czyli 0,618, np.:
   34 : 55 = 0,618,  377 : 610 = 0,618

   Ciąg Fibonaciego należy do ulubionych ciągów spotykanych w  przyrodzie – można go odnaleźć w wielu jej aspektach – zarówno w kształtach fizycznych struktur, jak i w przebiegu zmian w strukturach dynamicznych.
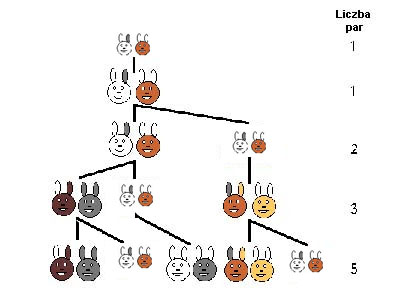
   Zmiany dynamiczne pod tym względem najlepiej charakteryzuje rozmnażanie się królików. Przy założeniu, że początkowo mamy jedną parę młodych królików– samca i samicę, które po miesiącu staną się dorosłymi, by po następnym miesiącu wydać na świat potomstwo. Po kolejnym miesiącu ich potomstwo wydorośleje i będzie zdolne do reprodukcji, rodzice zaś nadal się rozmnażają, łatwo policzyć roczny przyrost królików w sposób charakterystyczny dla naszego ciągu. Spójrzmy na tabelkę:

  
Widać z tego, że każda para dorosłych królików co miesiąc wydaje na świat parkę młodych, które po miesiącu, będąc już zdolne do rozrodu, rozmnażają się w analogiczny sposób, przy czym wciąż rodzą się młode z poprzednich par.

   Okazuje się, że ta błaha z pozoru zależność często odzwierciedlana jest w przyrodzie. Przyjrzyjmy się trutniom. Samiec pszczoły w przeciwieństwie do samicy (królowej, która ma zarówno ojca, jak i matkę – inną królową) powstaje wyłącznie dzięki matce. Jak więc wygląda jego drzewo genealogiczne?

samiec ---- samica                samica         samiec ---- samica
             I                                  I                         I
         samica                         samiec  ----------  samica
             I                                               I
         samiec  ---------------------------  samica
                                    I
                               samica
                                    I
                               samiec

   Jak widać, przodkowie trutnia – jego matka, jej rodzice i dalej, aż po pradziadków, narastają zgodnie z zasadą ciągu Fibonacciego – kolejne pokolenia to suma dwóch poprzednich.
   Również wśród roślin występuje ta zależność. Przykładem może być wszędobylski krwawnik, którego pędy rozwijają się zgodnie z naszym ciągiem – w okresie kolejnych miesięcy ich przyrost zwiększa się w charakterystyczny sposób:

W ten sam sposób przyrastają gałęzie dębów czy innych drzew.

 
  Gdyby przyjrzeć się z bliska łuskom szyszki, ananasa, ziarnom na tarczy słonecznika czy kwiatom kalafiora – można zauważyć, że układają się spiralnie, a ich przyrost również podlega regułom słynnego ciągu – wystarczy policzyć liczbę prawo- i lewoskrętnych spiral –

pestki słonecznika czy różyczki kalafiora ułożone są wzdłuż logarytmicznych krzywych, które grupami biegną w różnych kierunkach, na przykład
34 lewoskrętne i 55 prawoskrętnych. A 34 i 55 to nic innego, jak liczby Fibonacciego

   W przypadku słonecznika również jego ulistnienie podporządkowane jest ciągowi Fibonacciego – liście wyrastają wokół łodygi, w maksymalny sposób wykorzystując dostęp do światła i wody spływającej wzdłuż łodygi, czyli – gdybyśmy spojrzeli z góry – jeden drugiego nie zasłania, bowiem cechują się spiralną filotaksją (ulistnieniem), a liście układają się wzdłuż helisy – spirali okrążającej łodygę. Określa się ją, licząc obroty, a także odległości między liczbami – dla wielu roślin te liczby są liczbami Fibonacciego.

 
  Jeszcze jedną ciekawostką dotyczącą ciągu Leonarda z Pizy jest spirala Fibonacciego. Najlepszym jej przykładem w przyrodzie są muszle. Gdyby spojrzeć na muszlę łodzika (morskiego mięczaka) w przekroju:

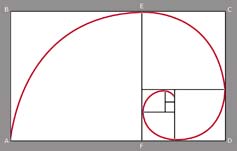
widać, że ułożona jest spiralnie i zbudowana z szeregu komór, z których każda następna jest większa od poprzedniej dokładnie o tyle, ile wynosi wielkość tej poprzedniej. Wynika to z faktu, że im są większe, tym szybciej rosną. Być może trudno uwierzyć, że układ muszli zgodny jest z jakimkolwiek ciągiem, ale wystarczy spojrzeć na graficzny obraz spirali Fibonacciego:

   Wyraźnie widać, że (pomijając dwa pierwsze, najmniejsze) kolejne kwadraty są większe od poprzedzających dokładnie o sumę ich ścianek, co zgodne jest z regułą naszego ciągu.

(ag)