|
|
 |
Propozycje rozwiązań ciekawych zadań
|
|
Tajemniczy pierwiastek Pod literami A; B; C; D; E; F; G; H; I ukrywają się cyfry 1; 2; 3; 4; 5; 6; 7; 8; 9. Wskaż jaka cyfra ukrywa się pod każdą z liter jeśli prawdziwa jest równość: |
|
Pojemność butli Butla wypełniona kwasem siarkowym ma masę M=19,34 kg. Ta sama butla tak samo wypełniona naftą ma masę m=9,1 kg. Jaka jest pojemność butli i jaka jest jej masa, gdy butla jest pusta, jeżeli gęstość kwasu siarkowego D=1834 kg/m3, a gęstość nafty d=810 kg/m3? Rozwiązanie: Niech v – objętość butli. Wówczas masa kwasu siarkowego wypełniającego butlę wynosi v * D. Jeżeli objętość będziemy mierzyć w litrach, to otrzymamy: masa kwasu siarkowego – 1,834 kg/l * v Podobnie masa nafty – 0,81 kg/l * v Oznaczmy przez x masę pustej butli Możemy wówczas napisać układ równań |
|
Po rozwiązaniu tego układu mamy: |
|
Odpowiedź: Pojemność butli wynosi 10 l, a masa pustej butli wynosi 1 kg. |
|
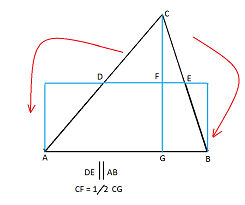
Zamiana trójkąta na prostokąt Dowolny trójkąt ABC rozetnij dwoma cięciami na trzy części, tak by z tych części można było złożyć prostokąt. Rozwiązanie: Popatrz na rysunek obok. |
 |
 |
|
Kwadrat i sześciokąty Podziel kwadrat na 4 przystające sześciokąty. Rozwiązanie: Popatrz na rysunek obok |
 |
 |
|
Gruba książka Do ponumerowania wszystkich stron pewnej księgi użyto 3389 cyfr. Ile stron liczy ta księga? Rozwiązanie: Na ponumerowanie 9 pierwszych stron użyto 9 cyfr.
3389-9= 3380
Na ponumerowanie dalszych 90 stron użyto 180 cyfr
3380-180=3200.
Na ponumerowanie dalszych 900 stron użyto 2700 cyfr
3200-2700=500.
Na ponumerowanie każdej następnej strony potrzeba 4 cyfr
500:4=125
Książka liczy więc 1124 strony. |
|
Polowanie na ryby W zatoce jeziora są wbite 2 pale. Jeden pal wystaje nad wodę na wysokość 2 m, drugi na wysokość 1 m. Odległość między palami wynosi 10 m. Na każdym palu siedzi ptak czatujący na rybę. Prędkość lotu ptaka siedzącego na wyższym palu jest dwukrotnie większa od prędkości lotu ptaka siedzącego na niższym palu. Gdy na linii łączącej pale plusnęła ryba, ptaki zobaczyły ją jednocześnie i jednocześnie rzuciły się po zdobycz. W którym miejscu plusnęła ryba, jeżeli obydwa ptaki dopadły ją jednocześnie. Rozwiązanie: W sklepie zoologicznym Właściciel sklepu zakupił pewną liczbę sztuk zajęcy i pewną liczbę par królików. Liczba par królików była równa połowie liczby zajęcy. Za każdego zająca właściciel sklepu płacił po dwa dolary, a za każdego królika po 1 dolarze. Cena detaliczna, którą brał, była o 10 % wyższa za każde zwierzę (2,2 dolara i 1,1 dolara). Gdy wszystkie zwierzęta z wyjątkiem 7 były sprzedane, właściciel sklepu stwierdził, że wyłożona na ich kupno kwota zwróciła się. Jego czysty zysk stanowi więc wartość sprzedaną owych siedmiu pozostałych zwierząt. Jaki jest czysty zysk właściciela sklepu? Rozwiązanie: Na czas
Internat pewnej szkoły znajduje się w znacznej odległości od niej i uczniowie muszą być wożeni do szkoły na godzinę 8 rano. Jeżeli autobus wiozący uczniów będzie jechał z prędkością 30 km/h, to zajedzie przed szkołę o 30 minut za wcześnie, jeżeli natomiast będzie jechał z prędkością 20 km/h, zajedzie o 30 minut za późno. Jaka jest odległość internatu od szkoły i z jaką prędkością powinien jechać autobus, aby zajechał przed szkołę punktualnie o godzinie 8 rano? Rozwiązanie: Niech t – czas od momentu wyjazdu spod internatu do momentu rozpoczęcia pierwszej lekcji w szkole. s – odległość internatu od szkoły W przypadku, gdy autobus jechał 30 km/h s = 30 * (t – 0,5) = 30t – 15 W przypadku, gdy autobus jechał 20 km/h s = 20 * (t + 0,5) = 20t +10 Więc 30t -15 = 20t +10 / - 20t + 15 10t = 25 / : 10 t = 2,5 Wyznaczmy s s = 20 * (t + 0,5) = 20 * (2,5 + 0,5) = 20 * 3 = 60 Policzmy średnią prędkość autokaru 60 = v * 2,5 / * 10 600 = v * 25 v = 600 / 25 v = 24 Odp: Średnia prędkość autokaru powinna wynosić 24 km/h, a odległość między autokarem, a szkołą wynosi 60 km. |
|
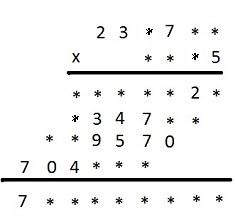
Tajemniczy iloczyn Odtwórz następujący iloczyn.
Rozwiązanie |
 |
 |
|
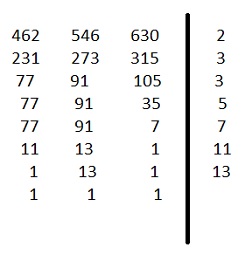
PODRÓŻE WAKACYJNE Przez pewną stację przejechały trzy pociągi specjalne, wiozące młodzież szkolną na kolonie. W pierwszym pociągu na kolonie jechało 462 dzieci; w drugim 546 dzieci, a w trzecim 630 dzieci. Oblicz z ilu wagonów składał się każdy pociąg, jeżeli wiadomo, że w każdym wagonie jechało tyle samo młodzieży i była to największa z możliwych liczba jadących w jednym wagonie. Rozwiązanie: |
|
Liczba jadących dzieci w każdym wagonie to największy wspólny dzielnik liczb 462; 546 i 630. czyli NWD(462; 546; 630)=42. W każdym wagonie jechało po 42 dzieci. Pierwszy pociąg liczył 462:42= 11 wagonów; drugi pociąg liczył 546:42=13 wagonów i trzeci pociąg liczył 630:42=15 wagonów. |
 |
 |
|
PODZIAŁ PIENIĘDZY Dwaj farmerzy: Adam i Bartek sprzedali stado owiec biorąc za każdą owcę tyle talarów, ile było w stadzie owiec. Zarobionymi pieniędzmi postanowili podzielić się po połowie. Najpierw podzielili między siebie banknoty. Po podziale banknotów okazało się, że Adam dostał o 10 talarów więcej niż Bartek. Pozostałe w bilonie pieniądze zabrał więc Bartek. Jednak, było tej reszty mniej niż 10 talarów. Aby powetować Bartkowi straty, Adam pozwolił mu jeszcze zabrać sakiewkę. Oblicz, jaka była wartość sakiewki. Rozwiazanie Załóżmy, że owiec w stadzie było 10a+b, gdzie b jest liczbą jednocyfrową.
Wówczas, za sprzedane owce Adam i Bartek dostali |
|
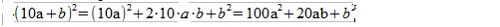 |
talarów.
W pierwszym i drugim składniku otrzymanej sumy jest na pewno parzysta ilość 10-talarówek. Da więc się sprawiedliwie rozdzielić pomiędzy Adama i Bartka. Ponieważ jednak Bartek dostał o jedną 10-talarówkę mniej, więc jednocyfrowa końcówka ilości owiec b, musi być tak dobrana, by b^2 było liczbą dwucyfrową i taką by cyfra dziesiątek tej liczby była nieparzysta. Jak łatwo sprawdzić warunek ten spełniony jest dla b = 4 i dla b = 6.
Ponieważ jednak 4^2=16 i 6^2=36, więc w rozliczeniu Bartek dostał jeszcze 6 talarów i sakiewkę wartą 4 talary. |
|
GŁĘBOKOŚĆ DOŁU Na pytanie przechodnia o docelową głębokość dołu kopanego właśnie przez robotnika, kopacz udzielił następującej odpowiedzi: „mój wzrost wynosi 1m i 80 cm. Gdy wykopię dół do końca, moja głowa będzie o tyle poniżej powierzchni ziemi, o ile teraz gdy już wykopałem połowę głębokości dołu, jest powyżej niej”. Jaka będzie głębokość dołu? Rozwiązanie: x – głębokość połowy dołu
y – wysokość na jaką wystaje robotnik stojący w kopanym dole.
Zachodzi więc równanie:
x+y=1,8 m (wysokość robotnika)
Po wykopaniu całego dołu będzie on miał głębokość 2x, głowa robotnika będzie schowana y od powierzchni chodnika. Zachodzi więc następujące równanie
2x=1,8 m+y.
Należy więc rozwiązać następujący układ równań: |
|
Rozwiążmy ten układ równań |
|
Czyli dół będzie miał głębokość 2x = 2,4 m |
|
ILE MIAŁEM PIENIĘDZY Wychodząc z domu miałem w kieszeni pewną liczbę złotówek i pięciozłotówek. Razem było więcej niż 140 zł, ale mniej niż150 zł. Wydałem trzecią część posiadanej gotówki. Po powrocie stwierdziłem, że pozostało mi tle złotówek ile przed wyjściem miałem pięciozłotówek i tyle pięciozłotówek ile początkowo miałem złotówek. Oblicz, ile pieniędzy miałem wychodząc z domu? Ile było tam złotówek, a ile pięciozłotówek? Rozwiązanie: Niech
x – ilość pięciozłotówek
y – ilość jednozłotówek
Wówczas ilość posiadanych pieniędzy opisuje wyrażenie 5x+y.
Ponieważ wydałem 1/3 swoich pieniędzy więc obecnie posiadam
5x+y-1/3(5x+y).
Z treści zadania wynika, że mam teraz tyle jednozłotówek ile przed wyjściem miałem pięciozłotówek i tyle pięciozłotówek ile przed wyjściem miałem jednozłotówek. Prawdziwe więc jest równanie
5x+y-1/3(5x+y)=5y+x.
Przekształćmy następujące równanie
15x+3y-5x-y=15y+3x
10x+2y=15y+3x
13y=7x
y=7(x/13).
Ponieważ x i y są liczbami całkowitymi naturalnymi, więc x/13 musi być całkowite, czyli x może być jedną z liczb: {13; 26; 39; 52; 65; …}. Wówczas y będzie odpowiednio równe: {7; 14; 21; 28; 35; …}.
Mając 13 pięciozłotówek i 7 jednozłotówek miałbym w sumie 72 zł
Mając 26 pięciozłotówek i 14 jednozłotówek miałbym w sumie 144 zł
Mając 39 pięciozłotówek i 21 jednozłotówek miałbym w sumie 216 zł
Wychodząc z domu miałem 144 zł, to jest 26 pięciozłotówek i 14 jednozłotówek. Wydałem 46 zł. Pozostało mi 98 zł, czyli 14 pięciozłotówek i 26 jednozłotówek. |
|
TAJEMNICZA LICZBA
Na miejscu jednostek pewnej trzycyfrowej liczby stoi cyfra 2. Jeżeli tę cyfrę przeniesiemy na pierwsze miejsce, to otrzymamy liczbę, która od pierwotnej będzie o jedną trzecią większa. Jaka to liczba?
Rozwiązanie Szukaną liczbę, można opisać wyrażeniem: 10x+2
Nową liczbę, którą otrzymamy po przestawieniu cyfr opisuje wyrażenie: 200+x.
Na podstawie warunków zadania zachodzi równanie: 4/3(10x+2)=200+x
Rozwiązując te równanie otrzymamy: x=16.
W takim razie szukana liczba początkowa, to 162, a otrzymana liczba po przestawieniu cyfr to 216.
TRUDNA ZAPŁATA
Kupujący ma zapłacić 37 zł. Problem jednak polega na tym, że kupujący ma w swoim portfelu same pięciozłotówki, a sprzedawca same dwuzłotówki. Pomóż im się rozliczyć.
Rozwiązanie
Niech
x – ilość pięciozłotówek wydanych przez kupującego.
y – ilość dwuzłotówek wydanych przez sprzedawcę.
Kupujący zapłacił 5x złotych i otrzymał towar za 37 zł i 2y reszty.
Wynika z tego, że x musi spełniać następujące warunki:
1. musi być tak dobrane, by 5x>37
2. x musi być nieparzyste.
Odpowiedź: Każda ilość pięciozłotówek spełniająca powyższe dwa warunki jest dobra. Np. jeśli sprzedający zapłaci, płacąc 9 pięciozłotówkami wyda na towar 45 zł. Ponieważ towar kosztował 37 zł sprzedający będzie musiał zwrócić mu jeszcze 8 zł, czyli wyda mu 4 dwuzłotówki. |
|
ZAKUP NASION ZBOŻA. Właścicielami pewnej farmy jest trzech braci: Adam, Bogdan i Karol. Pewnego roku uzgodnili oni, że zakupią nasiona pszenicy, by obsiać swoje pole. Adam i Bogdan pojechali dokonać zakupu, a Karol pozostał by na czas nieobecności braci doglądać farmy. Bogdan zakupił 75 worków pszenicy, a jego brat 45 worków. W domu postanowili, podzielić koszta zakupu pszenicy na trzy równe części. Ile dolarów musiał dać Karol Adamowi, a ile Bogdanowi jeżeli jego wkład w zakup zboża wynosił 1400 $? ROZWIĄZANIE: Ponieważ Adam kupił 45 worków pszenicy, a jego brat 75 worków pszenicy, to razem zakupili 45+75=120 worków pszenicy. Z warunków zadania wynika, że na każdego z braci przypada po 40 worków pszenicy. Karol więc dostanie 5 worków od Adama i za tyle musi mu zapłacić. Resztę, to jest 35 worków dostanie od Bogdana. Dla łatwiejszych rachunków przyjmijmy, że 5 worków to jedna działka, wówczas Karol dostanie jedną działkę od Adama i 7 działek od Bogdana. Jeżeli udział Karola wynosi 1400 $, to oznacza, że jedna działka pszenicy kosztuje 175 $, i tyle Karol musi zapłacić Adamowi. Resztę, to jest 1225 $ zapłaci Bogdanowi.
|
|
MISTRZOWIE LOGICZNEGO MYŚLENIA Staszek i Piotr uważani są w szkole za najlepszych matematyków. Aby rozstrzygnąć, który jest z nich najlepszy, nauczyciel wymyślił dwie liczby, a następnie policzył sumę tych liczb i ich iloczyn. Sumę z policzonych liczb zapisał na kartce i podał Staszkowi, a iloczyn zapisany na drugiej kartce podał Piotrowi. Poinformował też obu chłopców, że pomyślane przez niego liczby są większe niż 2. Następnie zapytał się, czy któryś z uczniów na tej podstawie potrafi podać liczby pomyślane przez nauczyciela.
Staszek powiedział, że nie wie jakie to liczby.
Na to Piotr mu odpowiedział: Wiedziałem, że nie będziesz znał liczb, ale nie martw się, ja też ich nie znam.
Po tej wypowiedzi Piotra, Staszek stwierdził, że wie jakie to liczby.
Jakie liczby wymyślił nauczyciel? ROZWIĄZANIE: |
|
Ponieważ Staszek zna sumę liczb (x+y), to znałby odpowiedź natychmiast tylko wtedy, gdyby suma wynosiła 4 (2+2) lub 5 (2+3). Wtedy, kiedy Piotr (który zna x*y) wiedział, że Staszek nie zna odpowiedzi, dowiedział się, iż iloczyn musi mieć kilka rozkładów na czynniki dające dokładnie tę samą sumę. Gdy w tym momencie Piotr nie znał odpowiedzi, to wiemy, że iloczyn musi mieć więcej niż jedną parę rozkładów na czynniki. teraz Staszek już wie, że poszukiwane liczby, to 3 oraz 4, bo sąjedynymi liczbami spełniającymi powyższe kryteria.
|
|
TAJEMNICZE SUMY A; B; C to kolejne cyfry liczby trzycyfrowej ABC. Podobnie D; E; F to kolejne cyfry liczby trzycyfrowej DEF, a G; H; I to kolejne cyfry liczby trzycyfrowej GHI. Jakie cyfry ukrywają się pod literami A; B; C; D; E; F; G; H i I jeśli prawdziwa jest następująca suma: ABC+ DEF = GHI, ponadto każda cyfra jest inna i nie występuje cyfra zero Rozpatrz dwa przypadki.
a) liczba GHI jest możliwie najmniejsza
b) liczba GHI jest możliwie największa.
Podobnie przeanalizuj sumę ABC +DEF = GHIJ, uwzględniając, że jedna z cyfr jest zerem, lecz zerem nie jest ani cyfra A ani cyfra D ani cyfra G.
Dla uproszczenia przyjmij, że ABC ROZWIĄZANIE |
|
ŻYCIORYS DIOFANTOSA Młodość Diofantosa trwała 1/6 jego całego życia. Przez następne 1/12 swego życia Diofantos zapuszczał brodę. Dumny ze swej brody, przeżył następne 1/7 swego życia. Przez cały ten etap swojego dotychczasowego życia, Diofantos był kawalerem. 5 lat później, ożenił się i żona urodziła mu syna. Syn żył dokładnie połowę życia swego ojca. Diofantos zmarł 4 lata po śmierci syna. Ile lat żył Diofantos? ROZWIAZANIE Niech x - długość życia Diofantosa.
Wystarczy rozwiązać równanie:
1/6x +1/12x +1/7x +5 +1/2x +4 = x
Ostatecznie x = 84 Odpowiedź: Diofantos żył 84 lata. |
|
EFEKTYWNE ĆWICZENIA Edward lubi wykonywać fizyczne ćwiczenia. Wciągu jednej minuty jest wstanie wykonać 20 podciągnięć, lub 30 przysiadów, lub 40 pompek.
Wykonanie jednego podciągnięcia pozwala spalić 1,5 kalorii. Przy jednym przysiadzie spala 1,8 kalorii, a przy jednej pompce spala 1,2 kalorii.
Edward nie może poświęcać zbyt dużo czasu na ćwiczenia dlatego musi opracować dla siebie dwa plany ćwiczeń:
1. trening ekspresowy, który potrwa 7 minut i pozwoli na spalenie300 kalorii. W czasie tego treningu wykona 200 elementarnych ćwiczeń. Jedno elementarne ćwiczenie to: jedno podciągnięcie, lub jeden przysiad, lub jedna pompka.
2. Pełny trening. Ma on trwać co najmniej 30 minut, ma pozwolić spalić co najmniej 1200 kalorii, i powinien składać się z możliwie jak najmniejszej ilości ćwiczeń elementarnych.
Każdy rodzaj treningu powinien uwzględniać przynajmniej jedno elementarne ćwiczenie z każdej kategorii.
Oblicz ilość elementarnych ćwiczeń każdej kategorii, oraz całkowitą ilość ćwiczeń w każdym rodzaju treningu. Rozwiązanie: |
|
ZAMIANA POZYCJI CYFRY Gdy pomnożymy 102564 przez 4 to najbardziej na prawo położona cyfra przesunie się na skrajną lewą pozycję, a pozostałe cyfry przesuwają się o jedną pozycję w prawo (102564 x 4 = 410256). Znajdź najmniejszą liczbę, mającą tę samą własność, gdy pomnożona zostanie przez n, gdzie n to liczba całkowita od 2 do 9. Rozwiązanie:
OKRĄGŁY STÓŁ Trzysta osób siedzi wokół okrągłego stołu. Osoby są ponumerowane od 1 do 300 i każda osoba ma dwóch sąsiadów. Np.: sąsiadami pierwszej osoby są: osoba o numerze 2 i osoba o numerze 300; sąsiadami osoby o numerze 300 są osoby o numerach 299 i 1. Jest też 300 ponumerowanych kelnerów. Każdy kelner ma urnę z trzema kulami. Kule oznaczone są odpowiednio P; N; L. Kelner y wyciąga losowo kulę ze swojej urny i jeśli kula jest oznaczona jako P dostarcza deser sąsiadowi gościa o numerze y który siedzi po jego prawej stronie. Gdy wylosuje kulę oznaczoną literą N deser daje osobie y. Wylosowanie kuli znaczonej literą L powoduje, że deser od tego kelnera dostanie sąsiad osoby y siedzący po jego lewej stronie. Nazwijmy daną osobę szczęściarzem, jeśli otrzyma trzy desery. Znajdź największą możliwą liczbę szczęściarzy, oraz prawdopodobieństwo, iż tyle osób jest szczęściarzami. Rozwiązanie
Ponieważ przygotowanych jest 300 deserów (tylu jest gości), więc jeżeli szczęściarze dostaną po trzy desery, starczy ich dla 100 osób. Załóżmy przez moment, że trzy desery dostała osoba o numerze n. Zdarzy to się wówczas, gdy kelner o numerze (n-1) wylosuje kulę z literką P; kelner o numerze n wylosuje kulę z literką N i kelner o numerze (n+1) wylosuje kulę z literką L. Wynika z tego, że zdarzenie polegające na tym, że dokładnie 100 osób otrzyma po trzy desery może się zdarzyć na trzy sposoby:
Sposób pierwszy: potrójne desery otrzymają osoby o numerach: 3; 6; 9; 12; 15; 18; 21 itd.
Sposób drugi: potrójne desery otrzymają osoby o numerach: 2; 5; 8; 11; 14; 17; 20 itd.
Sposób trzeci: potrójne desery otrzymają osoby o numerach: 1; 4; 7; 10; 13; 16; 19 itd.
Prawdopodobieństwo, że dany kelner wylosuje oczekiwaną przez nas kulę wynosi 1/3. Prawdopodobieństwo, że wszyscy kelnerzy wylosują oczekiwaną przez nas kulę wynosi (1/3)^300. Ponieważ są trzy możliwości, więc prawdopodobieństwo, że 100 osób otrzyma potrójny deser wynosi 3*(1/3)^300=(1/3)^299. |
|
 |
 |
STATYSTYKA NA CO DZIEŃ
Z szuflady wyciągnąłem kilka pudełek z zapałkami i policzyłem ilość zapałek w każdym pudełku. Mediana, moda (dominanta) oraz średnia z tych obliczeń wyniosły odpowiednio: 3; 4 oraz 5. Jaka jest najmniejsza liczba pudełek które mogłem znaleźć w szufladzie?
Rozwiązanie: Warunek, że dominanta wynosi 4 zachodzi w dwóch przypadkach:
Przypadek I: w szufladzie było tylko jedno pudełko, w którym znajdowały się 4 zapałki.
Przypadek II: w szufladzie było więcej niż jedno pudełko, ale pudełek z czterema zapałkami było najwięcej.
W pierwszym przypadku, także mediana wynosiłaby 4, a ma wynosić 3, czyli pudełek było więcej niż jedno.
Gdyby w szufladzie były dwa pudełka, to aby dominanta wynosiła 4 w obu musiałoby być po 4 zapałki, ale wówczas i mediana wynosiłaby 4 a nie 3. Wniosek: pudełek było więcej niż dwa.
Gdyby w szufladzie były trzy pudełka, wówczas w co najmniej dwóch byłyby po cztery zapałki. Niezależnie od zawartości trzeciego pudełka, mediana także wynosiłaby 4, a nie 3.
Dopiero przy czterech pudełkach zapałek, można tak dobrać ich zawartość by dominanta wynosiła 4, a mediana wynosiła 3. Zachodzi to w dwóch przypadkach:
Przypadek I: jedno pudełko jest puste, jedno pudełko zawiera dwie zapałki i dwa pudełka zawierają po 4 zapałki;
Przypadek II: jedno pudełko zawiera jedną zapałkę, jedno pudełko zawiera dwie zapałki i dwa pudełka zawierają po 4 zapałki.
Jednak w obu przypadkach średnia ilość zapałek w pudełku jest mniejsza od 4, a ma wynosić 5.
Aby zachodził warunek, że średnia ilość zapałek w pudełku jest równa pięć i jednocześnie, by spełnione były dwa poprzednie warunki, musimy jeden z powyższych zestawów uzupełnić o co najmniej dwa pudełka, z których w jednym będzie mniej niż 3 zapałki, a w drugim więcej niż 5 zapałek.
Tak więc najmniejszą liczbą pudełek spełniających warunki zadania jest 6, wśród nich jedno pudełko jest puste, jedno zawiera jedną zapałkę, jedno zawiera dwie zapałki, dwa zawierają po 4 zapałki i jedno zawiera 19 zapałek. |
|
ZAKRĘCONE POTĘGI
Oto dwa niewinne pytania dotyczące wielomianów |
|
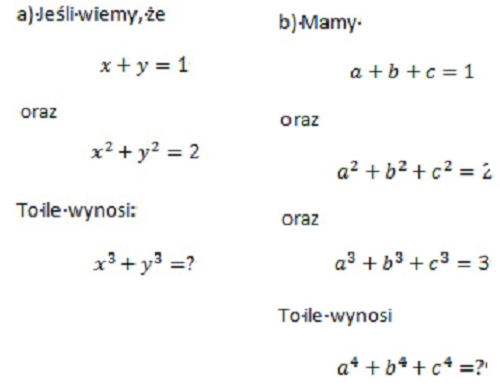 |
 |
Walentynki w kawiarni
Zaprosiłeś swoją wybrankę w walentynki do kawiarni. Niestety, tego dnia na podobny pomysł wpadło bardzo wiele zakochanych par. Przed drzwiami kawiarni utworzyła się już spora kolejka. Jesteś wraz ze swoją panią dziewiętnastą parą oczekującą na wolny stolik. Oszacuj, jak długo będziesz oczekiwał na wejście do kawiarni zakładając, że wewnątrz restauracji jest 40 stolików, a przeciętny czas pobytu przy stoliku jednej pary wynosi jedną godzinę. Rozwiązanie
Statystycznie jest bardzo mało prawdopodobne, by wszyscy siedzący przy stolikach goście zajęli, je jednocześnie. Dla ułatwienia obliczeń, możemy więc przyjąć, że gość, który zajął stolik najwcześniej właśnie kończy konsumpcję i lada moment zwolni stolik, natomiast ostatni gość z siedzących w lokalu zajął swoje miejsce w momencie gdy myśmy zajęli swoje miejsce w kolejce do lokalu, więc opuści go dokładnie za godzinę. Obliczmy więc średnią częstotliwość wymiany gości w lokalu.
1 godzina : 40 = 60 minut : 40 = 3/2 minuty = 90 sekund
Tak, więc statystycznie co 90 sekund z lokalu będzie wychodziła jedna para i do lokalu będzie wchodziła na ich miejsce nowa para. Ponieważ nie wiemy, ile czasu na konsumpcję pozostało jeszcze pierwszej parze, która po naszym przyjściu opuści lokal, (może ona wyjść w momencie, gdy my zajmiemy miejsce w kolejce, a może wyjść dopiero po 90 sekundach), najbezpieczniej będzie założyć, że ta pierwsza para opuści lokal 45 sekund po naszym przyjściu. Wtedy też do lokalu wejdzie para stojąca jako pierwsza w kolejce, a my będziemy już nie dziewiętnastą lecz osiemnastą parą czekającą w kolejce. Ponieważ następne pary gości będą się statystycznie wymieniać co 90 sekund, więc pozostaje nam jeszcze odczekać
90 sekund ∙ 18 = 1620 sekund = 27 minut. Po dodaniu jeszcze tych 45 sekund, otrzymujemy, że statystycznie biorąc nasz czas oczekiwania przed lokalem wyniesie około 27 minut i 45 sekund.
|
|
KÓŁKO I KRZYŻYK
W urnie jest 9 karteczek. Na tych kartkach znajdują się kolejno cyfry od 1 do 9. Losujemy trzy kartki bez zwracania. Następnie na diagramie obok stawiamy krzyżyki w polach o wylosowanych numerach. Jakie jest prawdopodobieństwo zdarzenia, że wszystkie krzyżyki będą się znajdować w jednej linii poziomej, lub pionowej, lub będą leżały na jednej z przekątnych diagramu.
|
 |
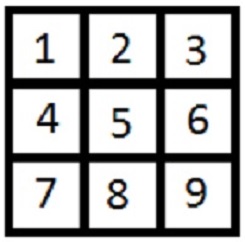 |
|
Rozwiązanie:
Pierwszą karteczkę można wylosować na 9 sposobów. Drugą karteczkę na 8 sposobów i ostatnią trzecią na 7 sposobów. Mamy więc 9∙8∙7 sposobów wylosowania trzech karteczek z pośród dziewięciu, przy uwzględnieniu porządku, w jakim te liczby zostały wylosowane. Ponieważ jednak, z treści zadania wynika, że kolejność losowania liczb jest nieistotna, ilość sposobów m wynosi więc:
m=(9∙8∙7)/3!=(9∙8∙7)/(3∙2∙1)=3∙4∙7=84
Z pośród tych 84 sposobów jest osiem sposobów, które są wygrywające. Oto one {(1; 2; 3); (4; 5; 6); (7; 8; 9); (1; 4; 7); (2; 5; 8); (3; 6; 9); (1; 5; 9); (3; 5; 9)}. Prawdopodobieństwo wynosi więc: P=8/84≈0,095
|
|
LICZBY DWUCYFROWE
Odgadnij następujące liczby dwucyfrowe, tak, by spełnione były następujące warunki.
a) Podwójna wartość liczby A jest większa od swojej połowy o 99.
b) Liczba B jest dwa razy większa od iloczynu swoich cyfr.
c) Liczba C jest trzy razy większa od sumy swoich cyfr.
d) Połowa liczby D jest większa od jednej trzeciej tej liczby o sumę jej cyfr.
e) Liczba E zwiększa się o 20%, jeżeli kolejność cyfr zostaje zmieniona.
f) Jeśli w liczbie F rozdzielimy jej cyfry, dopisując pomiędzy nie jeszcze dwie inne
cyfry to otrzymamy kwadrat liczby F.
g) Jeżeli w liczbie G zamienimy kolejność cyfr to otrzymamy liczbę, która różni się od G o podwojony iloczyn jej cyfr.
h) Iloczyn cyfr liczby H jest dwa razy większy od sumy cyfr tej liczby.
i) Jeśli liczbę I zapiszemy na kartce, a następnie kartkę z zapisaną liczbą odwrócimy do góry nogami, to zobaczymy liczbę większą od I o 12.
Rozwiązanie zadania
|
|
PARZYSTE, NIEPARZYSTE
Rozszyfruj następujący kryptarytm wiedząc, że P oznacza cyfrę parzystą, a N cyfrę nieparzystą. Rozwiązanie: |
 |
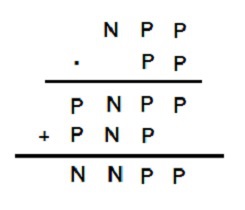 |
|
SILOS ZBOŻOWY Trzy silosy zbożowe mają następującą pojemność:
A – 8000 kg;
B - 5000 kg;
C – 3000 kg
A jest pełny, B oraz C są puste.
Czy potrafisz bez ważenia, przesypać 4000 kg do silosu A oraz 4000 kg do silosu B? ROZWIĄZANIE: |
 |
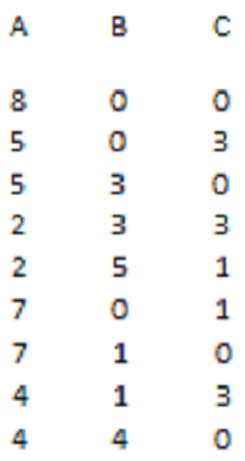 |
|
GRA W TRZY KOPERTY Jesteś uczestnikiem pewnej gry. Wejście do gry kosztuje 10 złotych. Gra polega na tym, że losujesz jedną kopertę spośród trzech. W jednej kopercie jest nagroda - 100 zł. Pozostałe dwie koperty są puste. Prowadzący pozwoli ci wybrać jedną kopertę, a następnie otworzy jedną z pozostałych kopert aby pokazać, że jest ona pusta. Następnie, prowadzący da ci wybór: pozostajesz przy swojej kopercie wybranej na początku, czy wybierasz pozostałą nieotwartą kopertę. Ponad to, oświadcza ci, jeszcze przed podjęciem przez ciebie decyzji, że jeżeli nie trafisz na pełną kopertę, to pozwoli ci jeszcze raz zagrać w tą samą grę bez dodatkowych opłat, jednak zwiększa tym razem zawartość wygrywającej koperty do 200 zł. Musisz, więc zadecydować: czy może lepiej przegrać pierwszą grę? Czy powinieneś zamienić kopertę? Następnego dnia, prowadzący informuje cię, jeszcze przed podjęciem przez ciebie gry, że jeżeli nie odnajdziesz pieniędzy w pierwszej rozgrywce, to pozwoli ci jeszcze raz zagrać, tym razem pula do wygrania będzie wynosiła 200 zł. Jeśli i tym razem też nie odnajdziesz pieniędzy, to możesz zagrać jeszcze trzeci ostatni raz. Tym razem o 300 zł. Gdy prowadzący poprosi cię o podjecie pierwszego wyboru - czy powinieneś zamienić kopertę, czy pozostać przy swoim początkowym wyborze?
Jakie decyzje będą dla ciebie najbardziej korzystne?
Rozwiązanie:
Ponieważ podany w zadaniu problem, będzie szczegółowo omówiony w jednym z najbliższych numerów "Świata Matematyki" dlatego tutaj ograniczę się tylko do lakonicznej odpowiedzi.
W pierwszej rozgrywce dla uczestnika korzystniejsze będzie nie dokonywać zmiany koperty licząc na to, że przegra. Zamianę koperty dokonać dopiero w drugiej rozgrywce (jeżeli do niej dojdzie) grając o 200 zł.
W drugim przypadku, dającym szansę na trzy rozgrywki i wygranie 300 zł w pirwszym podejściu należy nie zmieniać wybranej początkowo koperty (może przegramy i zyskamy prawo do dalszej gry o wyższe stawki). To jak postąpimy w drugiej turze (grając o 200 złotych) nie ma wpływu na wartość oczekiwaną naszej gry.
|
|
CZTERY EGIPSKIE UŁAMKI a; b; c; d to liczby naturalne. Znaleźć rozwiązanie następującego równania:
Ile istnieje takich rozwiązań?
Rozwiązanie
|
 |
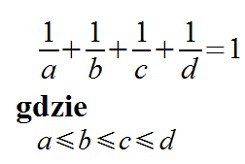 |
|
EGZAMIN TRZECH UCZNIÓW
Trzej uczniowie muszą zdać egzamin z n przedmiotów. Ilość punktów jest przyznawana zgodnie z miejscem w rankingu wyników egzaminu. Osoba, która najlepiej zda dany egzamin, czyli znajdzie się na pierwszym miejscu, otrzyma największą ilość punktów za ten egzamin, następny jest uczeń na drugim miejscu, a uczeń na ostatnim trzecim miejscu otrzymuje najmniejszą ilość punktów za dany egzamin.
Za I miejsce na egzaminie przyznawane jest x punktów, za II miejsce na tym egzaminie – y punktów, a za III miejsce – z punktów. Uczeń B otrzymał x punktów z j. polskiego. Uczeń A otrzymał w sumie 22 punktów. Uczniowie B oraz C otrzymali każdy w sumie po 9 punktów.
Z ilu przedmiotów zdawali uczniowie egzamin, oraz jakie są wartości x; y i z?
Rozwiązanie: |
|
MLEKO
Mamy beczkę mleka a potrzebujemy odmierzyć tylko 1 litr mleka.
Jak to wykonać, jeżeli mamy do dyspozycji naczynie o pojemności 3 litry oraz naczynie o pojemności 5-litrów? Rozwiązanie: Napełnij naczynie trzylitrowe mlekiem i przelej do pięciolitrowego naczynia. Następnie, napełnij ponownie naczynie trzylitrowe i mlekiem z tego naczynia uzupełnij naczynie pięciolitrowe. W naczyniu trzylitrowym pozostanie ci dokładnie litr mleka
|
|
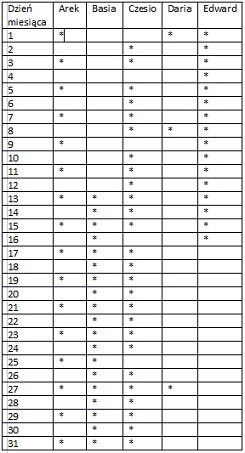
DZIEŃ SPOTKANIA Ponieważ moi przyjaciele z lat szkolnych mieszkają teraz w różnych miastach w całej Polsce, możemy się razem spotykać tylko raz do roku. Postanowiliśmy, że naszym miesiącem spotkań będzie zawsze sierpień. Natomiast dzień spotkania będzie co roku inny. Aby pamiętać o spotkaniu zaznaczaliśmy sobie dzień spotkania w kalendarzu. W tym roku nieszczęśliwie zgubiłem swój kalendarz z zaznaczoną datą spotkania. Postanowiłem więc zapytać o to moich kolegów. Niestety żaden z nich w czasie rozmowy telefonicznej ze mną nie miał pod ręką kalendarza z zaznaczoną datą i dlatego ich informacje były następujące:
Arek powiedział, że dzień spotkania jest liczbą nieparzystą
Basia stwierdziła, że liczba dnia jest większa od 13.
Czesio powiedział, że liczba dnia nie jest kwadratem żadnej innej liczby
Daria przysięgała, że liczba jest sześcianem pewnej innej liczby.
I na końcu Edward poinformował mnie, że data jest mniejsza od jednej czwartej jego wieku, który wynosi 68 lat.
Wczoraj dowiedziałem się, że tylko jedna z powyższych osób mówiła prawdę.
W jakim dniu odbędzie się spotkanie? Rozwiązanie: Aby ustalić dzień spotkania sporządźmy sobie tabelkę i nanieśmy informacje zebrane od znajomych w tej tabelce. Ponieważ zgodnie z informacją zawartą na końcu zadania, tylko jedna osoba mówiła prawdę, więc trzeba w tabelce znaleźć dzień wskazany tylko przez jedną osobę. Takim dniem jest oczywiście 4 sierpnia, czyli w tym dniu ma nastąpić spotkanie |
 |
 |
|
UCIECZKA PTAKÓW
W sklepie przyrodniczym, ktoś otworzył klatkę z ptakami i ponad 100 ptaków uciekło. Na początku w klatce było 300 ptaków. Miejscowa gazeta poinformowała, że z ptaków, które pozostały w klatce - 1/3 to zięby, 1/4 to papużki, 1/5 to kanarki, 1/7 to gwarki, oraz 1/9 to papugi. Początkowa ilość kanarków była trzy razy większa od ilości papug, które pozostały w klatce. Reporter artykułu pomylił się w jednym ułamku. Ile kanarków uciekło z klatki?
Rozwiązanie
Ponieważ przed ucieczką było w klatce 300 ptaków a uciekło ponad 100 ptaków, więc pozostało mniej niż 200. W takim razie ilość wszystkich ptaków jest wielokrotnością wszystkich mianowników podanych w zadaniu ułamków. |
|
Gdyby te ułamki były zgodne z prawdą ptaków powinno być co najmniej 1260, a wiemy, że jest ich mniej iż 200.
Jednak jeden z ułamków jest błędny. Nie wiemy, który, więc policzmy wszystkie możliwe przypadki.
Gdyby błędnie był podany ułamek pozostałych w klatce zięb, wówczas |
|
Gdyby błędnie był podany ułamek pozostałych w klatce papużek, wówczas |
|
Gdyby błędnie był podany ułamek pozostałych w klatce kanarków, wówczas |
|
Gdyby błędnie był podany ułamek pozostałych w klatce gwarków, wówczas |
|
Gdyby błędnie był podany ułamek pozostałych w klatce gwarków, wówczas |
|
Z wyliczonych wielokrotności najbardziej zgodna z warunkami zadania jest liczba 180. Zakładamy, więc, że błędnie został podany ułamek 1/7.
Z prostych rachunków wynika więc, że zięb pozostało w klatce 60; papużek pozostało w klatce 45; kanarków – 36 i papug 20, co stanowi 161 ptaków. Gwarków mogło zostać 19, co stanowi 19/180 pozostałych ptaków.
Ponieważ przed ucieczką kanarków było 3 razy więcej, niż jest obecnie papug, więc było ich 60. Pozostało w klatce 36, więc uciekły 24 kanarki. |
|
|
 |
|

