|
|
 |
 |
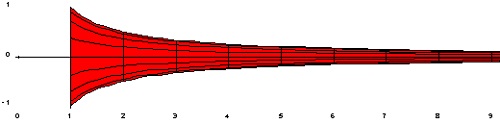
Istnieją obiekty w 3D mające nieskończoną powierzchnię bryły, ale skończoną objętość. Takim obiektem jest róg Gabriela. Można napełnić go farbą, ale nie będzie jej wystarczająca ilość aby pokryła zewnętrzną powierzchnię. Róg wydłuża się w nieskończoność, więc nie ma końca jej powierzchnia. Można go jedynie napełnić farbą, gdyż obiekt staje się coraz węższy wydłużając się w prawo i objętość zbliża się do skończonej wartości.
Róg Gabriela (lub trąbka Torricellego) – bryła geometryczna, opisana przez Evangelistę Torricellego, o nieskończonej powierzchni zewnętrznej, ale skończonej objętości. Nazwą nawiązuje do archanioła Gabriela, który wg tradycji chrześcijańskiej ma ogłosić Sąd Ostateczny zadęciem w róg.
Róg Gabriela jest bryłą obrotową ograniczoną przez powierzchnię powstałą w wyniku obrotu wokół osi OX wykresu funkcji
F(x) = 1/x
określonej w przedziale [ 1 , ∞ ] . Dzięki doborowi dziedziny funkcji f wykres tej funkcji ma tylko jedną asymptotę, którą jest oś rogu Gabriela. |
|
 |
2. PARADOKS BANACHA-TARSKIEGO.
|
|
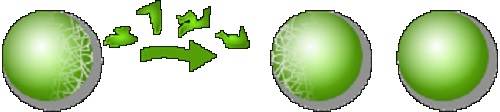
Można podzielić sferę na części, a następnie połączyć te części aby otrzymać dwie sfery, które są dokładnie takie same jak pierwsza sfera. Paradoks Banacha-Tarskiego Paradoks Banacha-Tarskiego: Kula może być pocięta na skończenie wiele kawałków, z których można złożyć dwie kule identyczne z kulą wyjściową Paradoks Banacha-Tarskiego (paradoks Hausdorffa-Banacha-Tarskiego, paradoksalny rozkład kuli) – paradoksalne twierdzenie teorii miary sformułowane i udowodnione przez Stefana Banacha i Alfreda Tarskiego w 1924 roku. Twierdzenie głosi, że trójwymiarową kulę można „rozciąć” na skończoną liczbę części (wystarczy ich sześć), a następnie używając wyłącznie przesunięć i obrotów można złożyć z tych części dwie kule o takich samych promieniach jak promień kuli wyjściowej. Paradoksalne jest to, że z jednej strony w wyniku operacji rozcinania, przesunięcia, obracania i składania następuje podwojenie objętości kuli, z drugiej użyte operacje przesunięcia i obrotu są izometriami i zachowują objętość brył. Źródło paradoksu tkwi w tym, że części, na które dzielona jest kula, są zbiorami niemierzalnymi (w sensie Lebesgue’a) tj. nie mają objętości i nie stosuje się do nich addytywność miary, zgodnie z którą suma miar rozłącznych zbiorów mierzalnych jest miarą sumy mnogościowej tych zbiorów. Paradoks Banacha-Tarskiego ma swoją popularną wersję: ziarnko grochu może być podzielone na skończenie wiele części, z których (przez izometrie) można złożyć kulę wielkości Słońca. |
|
 |
Fred przynosi do domu 100 kg ziemniaków, które (będąc ziemniakami czysto matematycznymi) składają się w 99% z wody. Następnie zostawia je na noc na zewnątrz, aby w 98% składały się z wody. Jaka jest ich nowa waga? Zaskakująca odpowiedź to 50 kg. Proste wyjaśnienie: Jedno wyjaśnienie zaczyna się od stwierdzenia, że początkowo waga bez wody wynosi 1 kg, co stanowi 1% ze 100 kg. Wtedy ktoś pyta: 1 kg to 2% z ilu kilogramów? Aby ten procent był dwukrotnie większy, całkowita waga musi być o połowę mniejsza. W tym pytaniu masa nie-wody nie może rosnąć ani się zmniejszać, dlatego zawsze będzie wynosić 1 kg, a masa wody musi się zmieniać wokół niej. Wyjaśnienia z wykorzystaniem algebry: Pozostała całkowita ilość po odparowaniu wody zawiera 1 kg czystych ziemniaków i (98/100) x wodę. Równanie wygląda następująco: 1 + (98/100)x = x => 1 = (1/50)x co daje = 50 kg. Implikacja Odpowiedź jest taka sama, o ile stężenie części niewodnej jest podwojone. Na przykład, jeśli ziemniaki pierwotnie zawierały 99,999% wody, zmniejszenie tego odsetka do 99,998% nadal wymaga zmniejszenia o połowę wagi. |
|
4. SKŁADANIE KARTKI PAPIERU |
|
Jeżeli złoży się standardowy arkuszu papieru na pół 103 razy, to grubość będzie większa niż rozmiar obserwowalnego wszechświata.
Inne wielkości:
23 złożenia na pół daje około 1km.
42 złożenia równe jest około odległość z Ziemi do Księżyca.
53 złożenia równe jest około odległość z Ziemi do Słońca. |
|
5. CIAGI ZBIEŻNE I ROZBIEŻNE |
|
1 + 1/2 + 1/4 + 1/8 + 1/16 + … równa się 2, ale
1 + 1/2 + 1/3 + 1/4 + 1/5 + … to nieskończoność. |
|
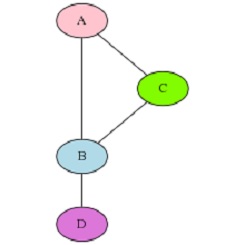
Przykładowy socjogram, w którym trzy z czterech osób mają niższą liczbę połączeń od arytmetycznej średniej połączeń sąsiadów (A i C obserwują średnią 2,5, D średnią 3).
Paradoks przyjaźni – paradoks w socjologii, zgodnie z którym większość osób zauważa, że większość ich przyjaciół średnio ma więcej przyjaciół niż oni sami. Paradoks został zaobserwowany i opisany w 1991 roku przez Scotta L. Felda, socjologa ze State University of New York. |
 |
 |
|
Zjawisko wynika z matematycznych właściwości sieci społecznych i jest bezpośrednio związane z nierównością między średnią arytmetyczną i geometryczną, oraz nierównością Cauchy’ego-Schwarza. Przekłada się także na inne typy relacji i skorelowanych z nimi cech w takich sieciach, na przykład przeciętną liczbę partnerów seksualnych, publikacji naukowych, wyższy poziom zadowolenia z życia, konsumpcji alkoholu itp. Paradoks może pogłębiać złudzenie powszechności wybranych cech w całym społeczeństwie, zwłaszcza w regionach sieci społecznych, które powstały na bazie podobieństw charakteru lub opinii.
W 2012 roku paradoks został zilustrowany na bazie realnych danych socjometrycznych przez badaczy z Cornell University, którzy przeanalizowali 721 mln użytkowników portalu Facebook[4]. W badaniu użytkowników Twittera wykazano, że zasada sprawdza się w przypadku 98% użytkowników portalu.
|
|
7. O PEWNEJ LICZBIE ZŁOŻONEJ |
|
2^67 -1 była uważane przez dłuższy czas jako liczba pierwsza (sugerowane przez Mersenne’a), aż gdy matematyk Frank Nelson Cole udowodnił, że tak nie jest czemu poświęcił wszystkie niedziele przez 3 lata.
Na konferencji matematycznej w 1903 roku, podszedł do tablicy i przed pełną widownią matematyków i w całkowitej ciszy napisał 147 573 952 589 676 412 927, co równa się 2^67 -1,
a następnie po drugiej stronie tablicy zapisał 193 707 721 x 761 838 257 287. Następnie wykonuje całe obliczenie ręcznie co wyniosło również 2^67 -1.
Odkłada kredę i w ciszy wraca do swojego miejsca. Po chwili rozlega się burzliwa owacja na stojąco. |
|
Zgodnie z prawem Zipfa: w dostatecznie dużej próbce tekstu z dowolnego języka – najczęściej występujący wyraz będzie występował dwa razy częściej niż wyraz na drugim miejscu, trzy razy częściej niż wyraz na trzecim miejscu, cztery razy częściej niż wyraz na czwartym miejscu, itp.
Prawo Zipfa lub prawo Estoupa-Zipfa – prawo opisujące zasadę częstotliwości użycia
w dowolnym języku poszczególnych wyrazów. Głosi ono, że jeżeli dla jakiegokolwiek tekstu lub grupy tekstów ustala się wykaz wyrazów ułożonych w malejącym porządku częstotliwości ich występowania, to ranga (numer porządkowy) wyrazu jest odwrotnie proporcjonalna do częstotliwości, zatem iloczyn częstotliwości i rangi powinien być wielkością stałą.
Pod koniec XIX wieku francuski stenograf i leksykograf Jean-Baptiste Estoup, badając zasady stenografii, ustalił podstawowe zasady statystyczne dotyczące tekstu. Twierdzenia francuskiego badacza zweryfikował i uściślił amerykański lingwista, zwolennik filozofii analitycznej, George Kingsley Zipf.
Prawo Estoupa-Zipfa zostało matematycznie wyrażone w równaniu Estoupa-Zipfa:
r x f = constans
gdzie r jest to ranga wyrazu w tekście lub grupie tekstów, a f częstotliwość jego występowania.
Wartość stałej jest zależna od długości tekstu. Równanie ma zastosowanie przede wszystkim do tekstów o średniej długości. W dziełach krótkich tekst jest z oczywistych względów bardziej zróżnicowany, natomiast w tekstach długich – mniej, co wpływa na wartość stałej.
Wynikający z równania tzw. rozkład Zipfa stosowany jest jako wzorzec, niewystępujący
w praktyce w sposób idealny. Informuje on o rozkładzie teoretycznym wyrazów w tekście. Dane pochodzące z konkretnego tekstu lub zbioru tekstu tworzą rozkład empiryczny. Porównanie obu rozkładów pozwala na ocenę stylu autora lub autorów. Im większa jest różnica między rozkładem teoretycznym a empirycznym, tym styl autora jest bardziej niezrozumiały. Gdy odchylenia są minimalne, styl zbliża się do doskonałości.
Na przykład gdy w danym tekście 100. wyraz został użyty 314 razy, tzn. ( r x f = 31400 ) ,
z kolei 200. wyraz został użyty 158 razy (r x f = 31600), to odchylenie od normy między setnym a dwusetnym wyrazem – zgodnie z prawem Estoupa-Zipfa – wynosi około 0,008%. |
|
9. Jak zważyć liczbę PI
Problemem wyznaczania liczby pi zajmowaliśmy się już nie raz. Pan Krzysztof Maciasuk przysłał nam ciekawy materiał filmowy, pokazujący, jak za pomocą wagi kuchennej wyznaczyć wartość liczby pi. Znajdziesz go na https://www.youtube.com/watch?v=ZU1rmbV3kkA |
|
|
 |
|

