KONCHOIDA NIKOMEDESA
 

 
Równanie kartezjańskie:  (x – b)²(x² + y²) – a²x² = 0 
 

    Nazwa nawiązuje do kształtu muszli. Krzywę badał grecki matematyk Nikomedes ok. roku 200 p.n.e. Pracował on jako młodszy geometra. Odkrył konchoidę, która była ulubioną krzywą XVII wiecznych matematyków – była wykorzystana przy rozwiązywaniu problemów związanych z podwajaniem objętości sześcianów oraz trójsekcji kąta.
   Newton stwierdził, że konchoida powinna mieć status standardowej krzywej.

   Konchoida była wykorzystywana przy budowie starożytnych budynków. Pionowy przekrój kolumn miał kształt pętli w konchoidzie.

 
CYKLOIDA
 

 
Parametryczne równanie kartezjańskie:  x = at – h sin(t), y = a – h cos(t)
 

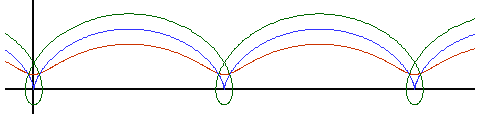
   Cykloida jest miejscem geometrycznym punktu położonego w odległości h od środka okręgu o promieniu a toczącego się bez poślizgu wzdłuż prostej linii. Jeżeli
h < a wtedy jest to cykloida skrócona (linia czerwona, zakreślana przez ustalony punkt leżący wewnątrz toczącego się koła), natomiast jeżeli
h > a jest to cykloida wydłużona (linia zielona, zakreślana przez ustalony punkt leżący na zewnątrz koła. Krzywa przedstawiona powyżej ma a = h.
 

 
   Po raz pierwszy cykloidę zbadał Cusa, w czasie jego poszukiwań wielkości powierzchni okręgu przy pomocy całkowania.
   Pierwszą poprawną definicję cykloidy podał Mersenne. Odkrył, iż długość podstawy cykloidy równa jest obwodowi toczącego się okręgu. Ponadto, bezskutecznie usiłował obliczyć powierzchnię pod krzywą przy pomocy całkowania.
   W 1599 r. Galileo nazwał niniejszą krzywę cykloidą. W 1639 r. napisał do Torricellego, iż studiował właściwości cykloidy przez 40 lat. Bezskutecznie usiłował również matematycznie obliczyć powierzchnię cykloidy poprzez porównywanie jej z tworzącym ją okręgiem.
W 1634 r. Roberval odkrył, iż jeżeli a = h wtedy powierzchnia pod łukiem wynosi
3 a² a długość jednego łuku cyklidy wynosi 8a.
   W 1658 r. Pascal, po długiej przerwie w pracach matematycznych  spowodowanej gorliwym oddawaniem się praktykom religijnym, zaczął rozmyślać o problemach matematycznych. Obliczył powierzchnię dowolnego wycinka cykloidy oraz jego środek ciężkości, jak również objętość i wielkość powierzchni bryły powstałej wskutek obrotu wokół osi x. Później Pascal ogłosił konkurs na rozwiązanie powyższych problemów oferując dwie nagrody. Sluze, Ricci, Huygens, Fermat oraz Wren przysłali rozwiązanie, ale bez oficjalnego angażowania się w konkursie.
   Cykloida ma tę właściwość, iż punkt przesuwający się po cykloidzie porusza się prostym ruchem harmonicznym właściwość ta została opisana przez  Huygens’a  w 1673 roku w pracy (Horologium oscillatorium). Skonstruował on pierwszy zegar wahadłowy z mechanizmem zapewniającym równookresowość ruchu wahadła dzięki wymuszeniu ruchu wahadła po łuku cykloidy.
   W 1639 roku Desargues zaproponował koła zębate z zębami wyciętymi w cyklodę.
   Zarówno ewoluta jak i ewolwenta cykloidy stanowią identyczną cykloidę. Dzięki badaniu ewoluty Huygens opracował ogólną teorię ewolut.

 
KRZYWA FIGURY ÓSEMKI
 

 
Równanie kartezjańskie:  x⁴ = a²(x² – y²) 
 
Układ współrzędnych biegunowych:  r² = a²cos(2) sec⁴()
 

   Krzywa ta jest również znana pod nazwą Lemniskata Gerono.

 
ELIPSA
 

 
Równanie kartezjańskie:  x²/a² + y²/b² = 1 
 
Równanie parametryczne:  x = a cos(t),  y = b sin(t)
 

   Elipsa po raz pierwszy była badana przez Menaechmus’a oraz Euklidesa. Ognisko i kierownicę elipsy badał Pappus.
   Kepler, w 1602 roku, wierzył, iż orbita Marsa tworzy owal, lecz później odkrył, że była to elipsa, w której ognisku znajdowało się Słońce. Odkrycie to opublikował w 1609 roku. Jednak ekscentryczność orbit planet jest niewielka, tj. są one kształtem zbliżone do okręgów. Ekscentryczność orbity Marsa wynosi 1/11 a Ziemi 1/60.
   W 1705 roku Halley wykazał, że kometa (obecnie nazwana jego imieniem) porusza się po orbicie eliptycznej wokół Słońca. Ekscentryczność komety Halley’a wynosi 0,a tor jest zbliżony do paraboli. Powierzchnia elipsy wynosi ab.  Nie ma dokładnego wzoru (funkcja elementarna) na długość elipsy. Problem ten badał Ramanujan i w 1914 roku podał wzór na przybliżoną długość:

 
(3(a + b) – [(a + 3b)(3a + b)]).
 

Ewoluta elipsy o podanym wyżej wzorze stanowi krzywa Lamé’go

 
(ax)^2/3 + (by)^2/3 = (a – b)^2/3.
 

   Z punktu położonego wewnątrz ewoluty (jest to zamknięta krzywa) można poprowadzić cztery normalne do elipsy, lecz z punktu położonego na zewnątrz – tylko dwie normalne